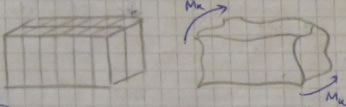
Кручение стержня некруглого поперечного сечения. Основные расчетные соотношения.

При кручении стержня произвольного поперечного сечения гипотеза плоских сечений не выполняется. Точки сечений смещаются продольно от первоначальной плоскости (депланация сечений).

Для сплошных сечений депланация незначительная, для тонкостенных незамкнутых профилей может быть весьма существенна.

Однако главное деформирование по-прежнему связано с перемещением точек в плоскости сечений, то есть с поворотом сечений вокруг оси z.

При свободном кручении стержня с некруглым сечением:

1) Повороты (), относительный угол закручивания () и энергию (U), можно считать по формулам проблемы Кулона ().

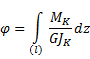
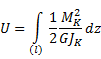
2) Депланации в сечениях малы и определяются методами теории упругости (или методами строймеха);

3) Геометрические характеристики Jк, Wк - не сводятся к расчету интеграла и определяются методами теории упругости;

4) Распределения напряжений по сечению индивидуальны для каждой формы сечений и определяются точным решением задачи о кручении (в частности распределение по сечению может быть существенно нелинейным).

В большинстве случаев внешний момент прикладывается к торцу стержня через некоторый конструктивный элемент, который не только передает момент, но и обеспечивает условия для W=0 (депланация равна 0). Такое кручение называется стесненным вследствие того, что в поперечном сечении возникают не только касательные напряжения (), но и нормальное напряжение , тогда:

Учет стесненности кручения ведется только для тонкостенной конструкции.