Напряженное состояние в точке. Главные площадки и главные напряжения. Определение главных напряжений в общем случае напряженного состояния.

В случаях сложного нагружения по принципу суперпозиций напряжение в точке можно найти наложением напряжения от простейшего нагружения.

Напряженное состояние в точке - это совокупность напряжений по всем площадкам, проходящих через данную точку.

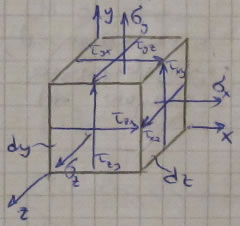
Из произвольно нагруженного тела вырежем элемент в форме куба и рассмотрим некоторое напряженное состояние.

На примере оси Х:

, - моментов не дают из уравнения равновесия (компенсируются на противоположной грани такими же напряжениями).

(аналогично для осей y и z)

Закон парности: , , .

В каждой исследуемой точке напряженного тела существует такая система осей x,y,z а которой касательне напряжения , , равны нулю. Такие оси называются главными осями, соответствующие им взаимно перпендикулярные площадки называются главными площадками, а нормальное напряжение на них - главным напряжением.

В порядке возрастания эти напряжения обозначают .

Определим главное напряжение и главные площадки для произвольного тензора напряжений.

Пусть площадка I - главная. Тогда , .

Применим теорему о напряженном состоянии.

- уравнение для нахождения главного напряжений и главных направлений

В координатном виде:

, l, m, n - неизвестные, но так как l, m, n - направляющие косинусы, то l² + m² + n² = 1, то есть l, m, n одновременно не равны нулю.

Полученная система является системо линейных однородных уравнений по отношению к l, m, n, имеющих нетривиальное решение.

Условие нетривиальности решения:

- характеристическое уравнение относительно .

- кубическое уравнение, позволяет найти главное напряжение.

Так как напряжение не зависит от ориентации осей в напряженном состоянии, то коэффициенты , , - являются инвариантами.

Если =0, то одно главное напряжение равно 0 (двухосное или плоское напряженное состояние).

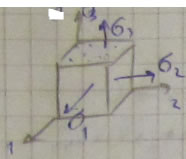
Если и равны 0, то два главных напряжения равны 0 (линейное или одноосное напряженное состояние)

Если напряженное состояние приведено к главным площадкам, то:

Для определения главных направлений, например соответствующего напряжению , в исходную систему подставляем найденное , а одно из уравнений заменяют связью между направляющими косинусами.