Напряженное состояние в точке. Теорема о напряженном состоянии в точке.

В случаях сложного нагружения по принципу суперпозиций напряжение в точке можно найти наложением напряжения от простейшего нагружения.

Напряженное состояние в точке - это совокупность напряжений по всем площадкам, проходящих через данную точку.

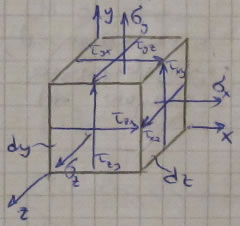
Из произвольно нагруженного тела вырежем элемент в форме куба и рассмотрим некоторое напряженное состояние.

На примере оси Х:

, - моментов не дают из уравнения равновесия (компенсируются на противоположной грани такими же напряжениями).

(аналогично для осей y и z)

Закон парности: , , .

Теорема о напряженном состоянии в точке: Напряженное состояние в точке определяется напряжениями по трем взаимно перпендикулярным площадкам проходящим через эту точку. Зная напряжение по трем взамно перпендикулярным площадкам можно найти напряжение в любой площадке.

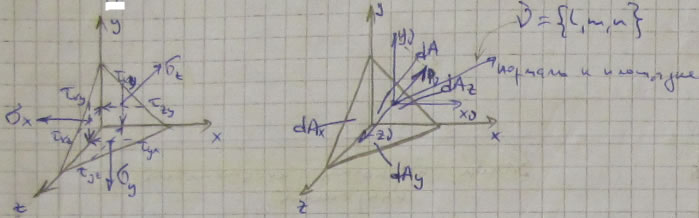
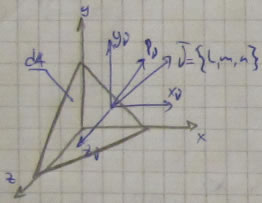
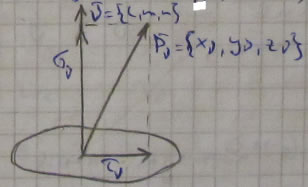
Проведем площадку с нормалью , где l, m, n - направляющие косинусы и площадью dA.

l=cos(, x) ; m=cos(, y) ; n=cos(, z)

По теореме о проекции: dAx=dA*l, dAy=dA*m, dAz=dA*m.

- уравнения равновесия

Для оси Х:

(аналогично для y и z)

Таким образом объект (тензор напряжений - симметричный тензор второго ранга) ставит в соответствие каждому направлению в пространстве определенный вектор.

Симметричность вытекает из закона парности (см. выше).

Для задания тензора необходимо знать: , , , , , .

- нормальное напряжение; - касательное напряжение.