Кручение стержня круглого поперечного сечения. Связь между крутящим моментом и углом поворота сечения.

Кручение - такой вид нагружения, при котором в поперечном сечении стержня возникает только крутящий момент (Mz / Mк).

Кручение вызывается:

1) сосредоточенным моментом вокруг оси стержня;

М - внешний момент; Мк - внутренний силовой фактор.

2) распределенным моментом вокруг оси z;

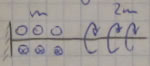
Распределенный момент возникает:

а) при передаче момента по длине;

б) при передаче момента с помощью сил трения.

3) любой поперечной нагрузкой приложенной не по оси стержня.

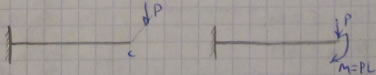
Данное нагружение - поперечный изгиб и кручение.

Основные гипотезы:

1) Плоские сечения. При кручении стержня круглого поперечного сечения, каждое сечение поворачивается как жесткое целое в своей плоскости на некоторый угол вокруг оси z. Это означает, что все точки сечения в процессе деформирования отаются в одной плоскости, а ось z при кручении не меняет своей геометрии.

2) В поперечном сечении при кручении возникают только касательные напряжения. Эта гипотеза выполняется всегда при свободном кручении.

В каждой точке поперечного сечения возникает напряженное состояние чистого сдвига.

Геометрические соотношения при кручении.

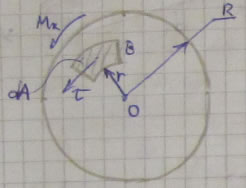
Рассмотрим стержень длиной dz и радиусом R, нагруженный крутящим моментом Мк.

По гипотезе 1, сечение II повернется вокруг оси z относительно сечения I на некоторый угол .

Вырежем из стержня трубку радиусом r и толщиной dr и рассмотрим ее подробнее.

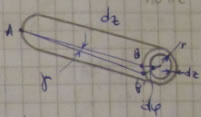
AB || z

Дуга , с другой стороны , следовательно , т.е. (деформация сдвига).

Из рисунка видно, что при перемещении точки В, образующая АВ сдвигается.

Введем величину - относительный угол закручивания (крутка).

Для каждого сечения величины и являются постоянными.

Связь между крутящим моментом (Мк) и углом поворота сечения ().

В окрестности точки В вырежем некоторый элемент.

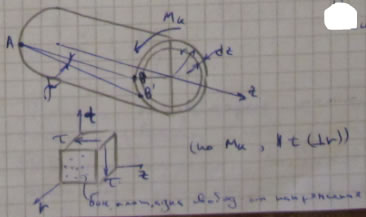
и связаны: - закон Гука для чистого сдвига.

Рассмотрим все сечение целиком.

- сила, r - плечо.

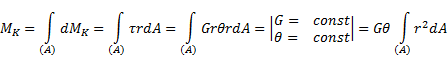
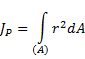
Jp - полярный момент инерции.

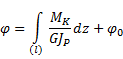
GJp - жесткость стержня при кручении.