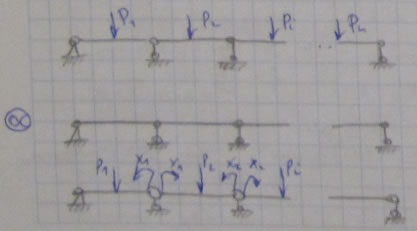
Расчет многопролетных балок. Уравнение трех моментов.

Вид канонических уравнений метода сил (КУМС) зависит от выбора основной системы (ОС).

Стремятся поступить так, чтобы упростить вычисление коэффициентов: 1) δ_ij , δ_ip - случай, если число неизвестных не велико; 2) получить систему удобной для вычисления структуры (пример: трехдиагональной) - случай большого числа неизвестных.

Обычно, если задача не типвая, то ОС стараются выбрать таким образом. чтобы эпюра Р была как можно проще.

Для типовых систем имеются стандартные методы решения.

Многопролетная балка:

В качестве ОС выбирают систему, полученную врезанием промежуточных шарниров, благодаря чему допускается взаимный поворот соседних стержней и каждый пролет можно рассматривать как независимый.

От каждого единичного силового фактора эпюра имеет вид треугольника, который стоится на смежных пролетах.

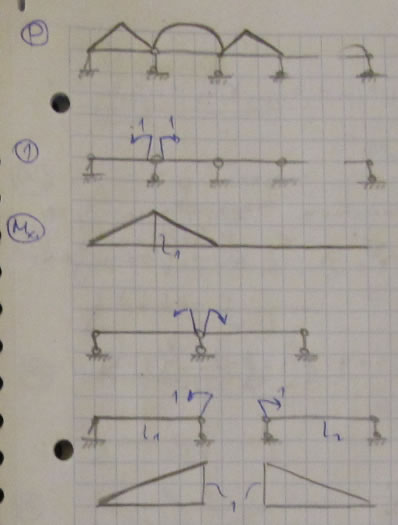
На каждом пролете эпюра строится из границы (граничных?) условий. Система канонических уравнений выражает отсутствие взаимных поворотов пролетов в промежуточных шарнирах. Выведем уравнение для i-го промежуточного шарнира.

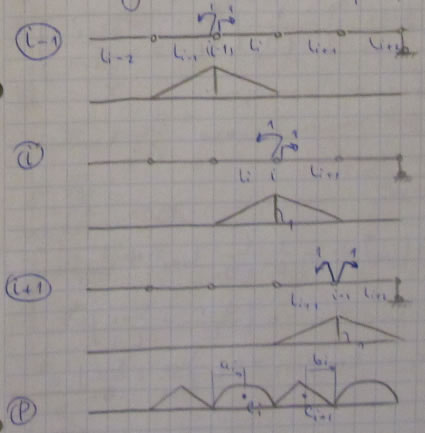
i-ое уравнение:

Так как эпюра (i) пересекается только с (i), (i-1), (i+1), то все коэффициенты кроме , , , равны нулю. Найдем коэффициенты , , методом Мора-Верещагина.

Найдем и из подобия.

;

и - статические моменты эпюры P на i-ом пролете относительно узла i-1 и эпюры P на (i+1)-м пролете относительно узла i+1.